
[Note: Consider only 2 decimal points if it necessary]
Objects
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
Weights
|
10
|
15
|
12
|
5
|
15
|
20
|
10
|
Profits
|
26
|
20
|
30
|
25
|
15
|
40
|
45
|
[ Note: We can execute one task at a time ]
Tasks
|
T1
|
T2
|
T3
|
T4
|
T5
|
T6
|
T7
|
T8
|
T9
|
T10
|
DeadLines
|
3
|
6
|
7
|
6
|
4
|
5
|
8
|
9
|
5
|
4
|
Profits
|
10
|
20
|
30
|
40
|
50
|
15
|
25
|
35
|
45
|
55
|
Suppose we have a Single Source Shortest Path on the following Adjacency Matrix with vertex 0 as the source.
Find out the total cost for reaching all other vertices from the source node for which the shortest path distances are finalized____ ?
Letter
|
A
|
L
|
G
|
O
|
R
|
I
|
T
|
H
|
M
|
Probability
|
20
|
18
|
16
|
12
|
10
|
6
|
5
|
2
|
1
|
Alice got a message in combination of 1’s and 0’s. Alice needs to apply a huffman code algorithm to understand the given message.
110100110011011110101
Find the decrypted message sent by Bob is____? [ Hint: consider left node as 0 ]
Objects
|
P
|
W
|
X
|
V
|
Q
|
R
|
T
|
S
|
Weights
|
18
|
10
|
15
|
20
|
12
|
16
|
16
|
14
|
Profits
|
36
|
18
|
26
|
32
|
18
|
22
|
20
|
16
|
60, 50, 45, 40, 35, 30, 15, 10.
Which of the following statements is false?
The recurrence relation for all pairs shortest path using dynamic programming technique is
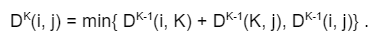
Given a directed weighted graph, Find the shortest distance matrix ‘D’.