Quiz Questions

Solve the limit:

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

Solve to 3 decimal places:

((0.083,0.084))

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

If f is a function on a set A= {1,2,3,4,5} such that f= { (1,1),(2,2),(3,3),(4,4),(5,5,)}. Then

f is bijective but not surjective

f is surjective but not injective

f is bijective

None of the above

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

Given f ( x ) = 3x^2−x+10 and g(x) = 1 − 20x find each of the following. [MSQ]

(f∘g)(5) = 29512

(f∘g)(1) = 1111

(g∘f)(2) = -359

(g∘g)(1) = 381

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

Given f (x) = 3x−2 and g(x) = x/3 + 2/3

Which of the following are true:

fog(x)= x

gof(x)= 2x

fog(x)= x/2

gof(x)= x

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

If A function f : A →B is an one to one function then

Number of elements in range of f is n

(b) n(A) = n(B)

Number of elements in range of f is n(A)

n(A) > number of elements in range of f

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

Evaluate

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

Evaluate

√2 /4

1/2√2

√2 /3

1/2

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

Evaluate

0.5

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

f(x) is defined as

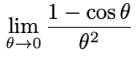
f’(0) is given by:

-9

-6

-5

-4

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

Evaluate

Solution to above limit is____?

√e

√e/2

√e/4

√e/6

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

⅛

⅝

-1/16

-6/16

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

Determine the value of ‘k’ for which the following function is continuous at x = 3:

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

f is continuous at x = 0, then find the value of a:

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.00

Find the value of k, for which f(x) is continuous at x = 0.

-1

-3

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

If the function f(x) given by

is continuous at x = 1, then find the values of a and b

a= 2,b=3

a= 3, b=2

a= 2, b=4

a= 4, b=2

Difficulty Level: 1

Positive Marks: 1.00

Negative Marks: 0.33

1/√2

1/√3

2/√2

4/√2

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

(Upto 2 decimals)

0.25

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.00

Find the values of a and b, if the function f(x) is differentiable at x = 1.

a= 3, b=5

a=5, b=3

a=2, b=3

None

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

If x = acosθ + bsinθ, y = asinθ – bcosθ, then find the value of

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.00

First two terms of the Taylor series for √ x centered at x = 1.

1+(x-1)/2

1+(x-2)/2

2+(x-1)/2

1+(x-4)/2

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

None

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

Find for what values of x, the function

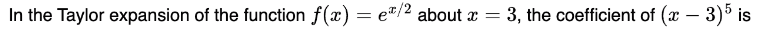
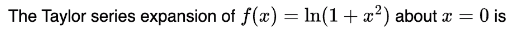
is increasing and for what values of x it is decreasing.

the function increases for x > 3

the function decreases for x < 3

the function decreases for x < 2

the function increases for x > 2

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

Find the maximum (local maximum) and minimum (local minimum) points of the function

Choose the correct option: [MSQ]

points of local maxima is (−1,5)

points of local maxima is (−2,5)

points of local minima is (3,−27)

points of local minima is (3,−23)

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

Find local maximum and local minimum, if any, of the following function

Choose the correct option:

local maximum at x = 1, 1/2

local minimum at x = – 1, -1/2

local minimum at x = – 2, -2/5

local maximum at x = 2, 2/5

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.00

Which of the following class of rectangles with given area always ensure least perimeter?

Square

Rhombus

Trapezoid

Isosceles Trapezoid

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

An open box with a square base is to be made out of a given quantity of sheet of area a^2. What’s the maximum volume possible?

a^3/(6√3)

a^3/(4√3)

a^2/(6√3)

a^2/(4√3)

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

A square metal sheet of side 48 cm. has four equal squares removed from the corners and the sides are then turned up so as to form an open box. Determine the size of the square cut so that volume of the box is maximum.

square of side 8cm

square of side 6cm

square of side 5cm

square of side 7cm

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

It is estimated that the operating rate of a major manufacturer's factories over a certain 365-day period is given by

percent. Determine the day on which the operating rate is maximized.

300

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.00

You are making cylindrical containers to contain a given volume. Suppose that the top and bottom are made of a material that is N times as expensive (cost per unit area) as the material used for the lateral side of the cylinder.

Find (in terms of N) the ratio of height to base radius of the cylinder that minimizes the cost of making the containers.

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

Marketing tells you that if you set the price of an item at $10 then you will be unable to sell it, but that you can sell 500 items for each dollar below $10 that you set the price. Suppose your fixed costs total $3000, and your marginal cost is $2 per item. What is the most profit you can make?

5000

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.00

You want to make cylindrical containers of a given volume V using the least amount of construction material. The side is made from a rectangular piece of material, and this can be done with no material wasted. However, the top and bottom are cut from squares of side 2r.so that 2(2r)^2= 8r^2 of material is needed (rather than 2πr^2 which is the total area of the top and bottom). Find the optimal ratio of height to radius.

8/π

9/π

4/π

5/π

Difficulty Level: 1

Positive Marks: 2.00

Negative Marks: 0.66

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution

Correct Answer

Solution