Consider a grammar G such that
S→aSb | bSa | ε
Suppose G1 is a grammar in CNF, equivalent to grammar G.
The number of steps required to derive the string “aaababbb” by the grammar G1 are _____
S1: Since every CFL is recursive, so we can use a Turing Machine to recognize a CFL.
S2: A language generated by type 2 grammar must be CFL and it cannot be regular.
Select the correct option.
G1: S→AB, A→a, B→b
G2: S→AB, A→a, B→C, C→b
Select the correct option.
Consider a grammar G such that
S→aSb | bSa | ε
Suppose G1 is a grammar in CNF, equivalent to grammar G.
The number of steps required to derive the string “aaababbb” by the grammar G1 are _____
Let L be a context free language. Then there exists a constant “n” (whose value depends upon L) such that for every string “z” belonging to the language L and |z| ≥ n, “z” can be broken into five parts “u”, “v”, “w”, “x” and “y” such that z=uvwxy and the three conditions. Select the three conditions from options.
S→AB
A→aAb
bB→bbbB
aAb→aa
B→ε
Select the correct language generated by this grammar from the options.
Select the correct option :
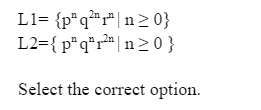
L1= {ww | w ε {a,b} }
L2= {ww | w ε {a,b}* }
Select the correct option
L1= {ww | w ε {a,b}* }
L2= complement (L1)
Select the correct option
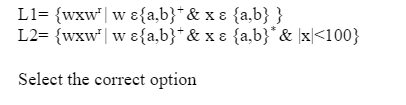
L = {x#w| x is prefix of w, where w∈{a,b}* }
Select the correct option.
If the input “aabbb” is given to Turing Machine then, what will be output and position of head when TM reaches a HALT state? Assume highlighted and underlined character depicts the head position at end and β represents a blank symbol.