The ratio in which the price at Rs 7.20 a kg be mixed with rice at Rs 5.70 a kg to produce a mixture worth Rs 6.30 a kg is:
A man can row with a speed of 12 kmph in still water. If the stream flows at 4 kmph, then the speed downstream is?
If a number is chosen at random from the set {11,12,13,14,...99},then the probability that the chosen number is a perfect square is:
The ratio in which the price at Rs 7.20 a kg be mixed with rice at Rs 5.70 a kg to produce a mixture worth Rs 6.30 a kg is:
What is the synonym of the word 'pitcher'?
Assertion (A): Plants are green.
Reason (R) : Plants contain chlorophyll which gives it the color green.
Find the odd one out.
Banquet, Carnival, Ravenous, Merry -making.
declare a stack of characters
while ( there are more characters in the word to read )
{
read a character
push the character on the stack
}
while ( the stack is not empty )
{
write the stack's top character to the screen
pop a character off the stack
}
What is written to the screen for the input "doodles"?
int(*ptr[5])();
#include <stdio.h>
typedef struct { int k; int l; int a[2]; } T;
typedef struct { int i; T t; } S;
T x = {.l = 43, .k = 42, .a[1] = 19, .a[0] = 18 };
// x initialized to {42, 43, {18, 19} }
int main(void)
{
S l = { 1,
.t = x,
.t.l = 41,
.t.a[1] = 17
};
printf(" %d\n", l.t.k);
}
#include<stdio.h>
struct Cricket
{
char team1[20];
char team2[20];
char ground[18];
int result;
}match[4] = {
{"IND","AUS","PUNE",1},
{"IND","PAK","NAGPUR",1},
{"IND","NZ","MUMBAI",0},
{"IND","SA","DELHI",1}
};
void main()
{
struct Cricket *ptr = match;
ptr+=2;
ptr--;
printf("\n%s Vs %s",ptr->team1,ptr->team2);
}
#include<stdio.h>
int main(){
int a[2][4]={3,6,9,12,15,18,21,24};
printf("%d %d %d",*(a[1]+2),*(*(a+1)+2),2[1[a]]);
return 0;
}
P: An arbitrary Directed Acyclic Graph(DAG) G=(V,E) is given as an adjacency list. Topological sort: the vertices of G can be completed in linear time?
Q: In the merge-sort execution tree, roughly the same amount of work is done at each level of the tree
Suppose we have a heap containing n = 2^k elements in an array of size ‘n’, and suppose that we repeatedly extract the minimum element, ‘n’ times, never performing insertions. To make the heap space efficient, we move the heap over to an array of size 2^j whenever an extraction decreases the number of elements to 2^j for any integer j. Suppose that the cost of each such move is Θ(2^j). What is the total movement cost caused by ‘n’ extract-mins starting from the heap of n elements? (Ignore the Θ(n log n) cost from the heapify operations themselves.)
Consider the following recursive implementation of the given problem
What will be the X and Y ?
The language accepted by the NFA is
r1: (a*b*)*
r2: b*a*
r3: ba*
The regular expression for L(r1) ∩ L(r2) ∩ L(r3) is:
S-> AB
A->aA | ϵ
B-> Bb | ϵ
Which of the following is/ are true about grammar G:
L1 ={<M,w> | M is a TM that accept w}
L2 ={<M,w> | M is a TM that doesn’t accept w}
Select the correct option.
Select the correct option
S→S+S /a
Select the correct option
S→ Ba | bBc | pc | bpa
B→p
Select the correct option.
L1= {w | w ϵ {a,b}* & number of (a) in w = number of (b) in w }
L2= { 0^n1^n | n >0 } UNION { 0^n1^2n | n >0 }
Select the correct option.

Schema I: Registration (rollno, courses)
Field ‘courses’ is a set-valued attribute containing the set of courses a student has registered for.
Non-trivial functional dependency: rollno → courses
Schema II: Registration (rollno, courseid, email)
Non-trivial functional dependencies:
rollno, courseid → email
email → rollno
Schema III: Registration (rollno, courseid, marks, grade)
Non-trivial functional dependencies:
rollno, courseid → marks, grade
marks → grade
Schema IV: Regstration (rollno, courseid, credit)
Non-trivial functional dependencies:
rollno, courseid → credit
courseid → credit
Which one of the relational schemas above is in 3NF but not in BCNF?
Course_Id
|
Course_Title
|
Course_Fee
|
C01
C02
C03
C04
|
Oracle
Java
C++
Oracle
|
8000
5000
4000
7000
|
What is the output of the following SQL query?
SELECT Count (*)
FROM (
(SELECT Course_Id, Course_Title
FROM Student) AS S
NATURAL JOIN
(SELECT Course_Title, Course_Fee
FROM Student) AS T
);
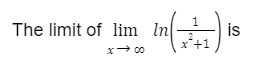
p: Pint is smart
q: Pint is honest
r: Pint is great
Then choose the correct translations. [MSQ]
is
Choose the correct statement/s
f(w,x,y,z)= Σ(1,5,6,7,11,12,13,15)
Which of the following statements is valid?
F(x,y)= x’y+xy’
G(x,y)= x+y
Which of the following statements is true?
M= 111100011000.
If Booth’s algorithm is used for multiplication, then the number of addition and subtraction operations required is______
f(w,x,y,z)= wx’ + wy’ + yz’
Which of the following are valid inputs? [MSQ]
f(x,y,z)= x ⊕y ⊕z is ___