
X = GOOGLE
Y = YAHOOE
A: Prim’s algorithm
B: Bellman Ford algorithm
C: Dijktra’s algorithm
D: Kruskal’s algorithm
E: Floyd Warshall
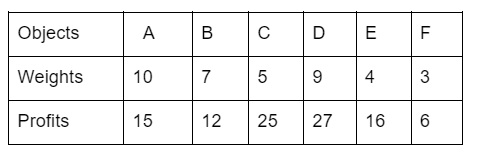
Item Name
|
Wight(in Kgs)
|
Profit(in rupees)
|
A
|
10
|
15
|
B
|
7
|
12
|
C
|
5
|
25
|
D
|
9
|
27
|
E
|
4
|
16
|
F
|
3
|
6
|
The maximum capacity of their bag size is 25. Alice has more intelligence than Bob. To get maximum profit Alice can also break the items. Bob can take an item or leave the item. According to the problem statement, apply a suitable algorithm and find the difference in maximum profit between Alice and Bob is_____[ [Note: Consider only 2 decimal points ]
60, 50, 45, 40, 35, 30, 15, 10.
Which of the following statements is false?
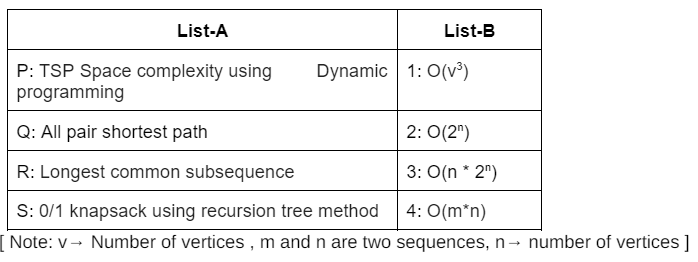
The recurrence relation for all pairs shortest path using dynamic programming technique is
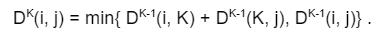
Given a directed weighted graph, Find the shortest distance matrix ‘D’.
[ Hint: For a subset of cities S ⊆ {1, 2, . . . , n} that includes 1, and j ∈ S, let C(S, j) be the
length of the shortest path visiting each node in S exactly once, starting at 1 and
ending at j. ]
P: For a dynamic programming algorithm, computing all values in a bottom-up fashion is asymptotically faster than using recursion.
Q: The running time of a dynamic programming algorithm is always Θ(P) where P is the number of subproblems.