T(n)= T(n/4) + T(n/2) + n^2
S1: f(n) = n^3
S2: g(n)= n^2 logn
S3: h(n)= n!
Which of the following statements is represented asymptotically correct?
Based on the given conditions which are asymptotically correct?
T(n)= T(n/4) + T(n/2) + n^2
T(n)= T(n-1)+1/n, if n>1
= 1, otherwise
The order of this algorithm is
Bob(int n)
{
for(i=n; i>=1; i=i/2)
for(j=1; j<=n; j=j*2)
printf("GATE 2021");
}
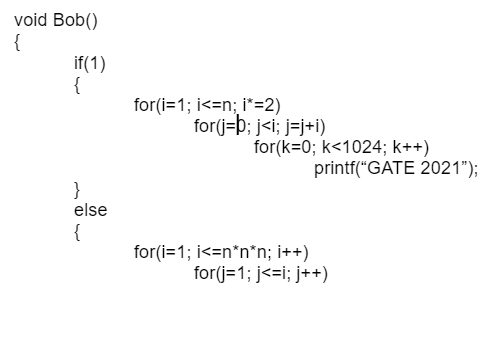
What is the complexity for the above given function?

int Bob(int n)
{
if(n==-1 || n==0 || n==1)
return 1;
if((n%2)==0)
return Bob(n/2)+Bob(n/2);
else
return 3*Bob(n/2)+Bob(n/2);
}


Bob(int n, int a, int b, int c)
{
if(n==1)
return 1;
else
{
Bob((n-1), a, c, b)
printf(“GATE 2021’);
Bob((n-1), c, b, a)
}
}

S1: 2T(n/2)-4T(n/2)+1 is solvable by using the master's theorem.
S2: If for an algorithm time complexity is given by O((3⁄2)^n) then complexity will be linear.
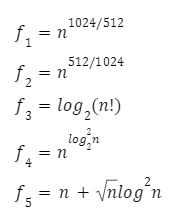
Flowchart for recursive function A(n):
T(n) = √(4) T(n/2) + √n
T(1) = 1
Find the worst case time complexity of given recurrence relation is O(n^𝛼)), then the least possible value (accurate upto two decimal positions) of α is _________.